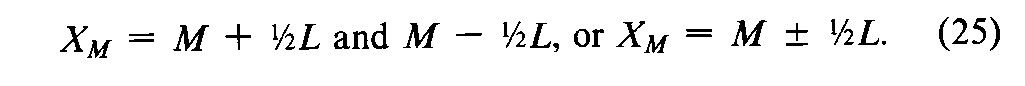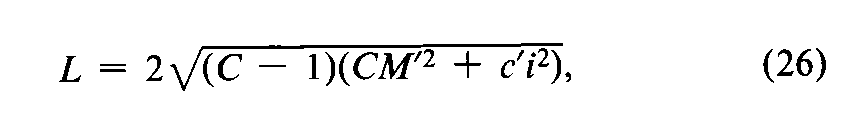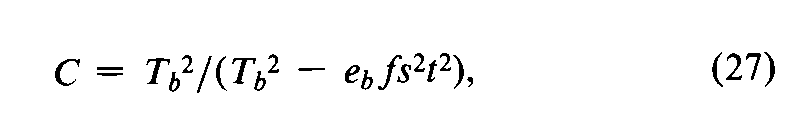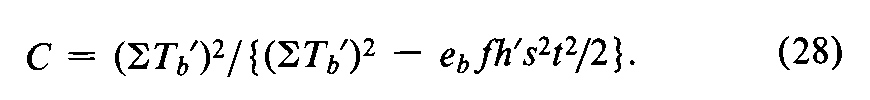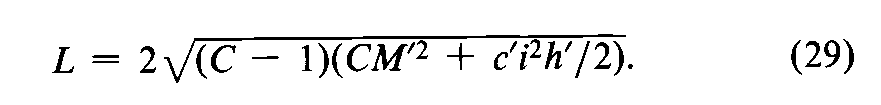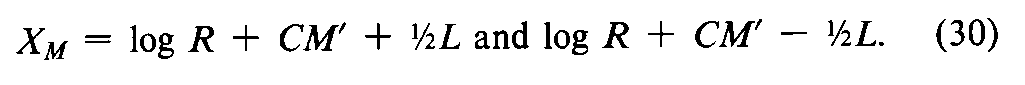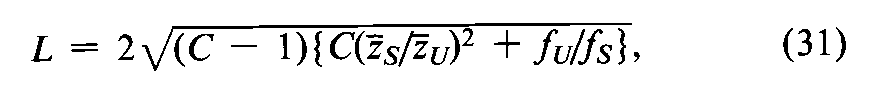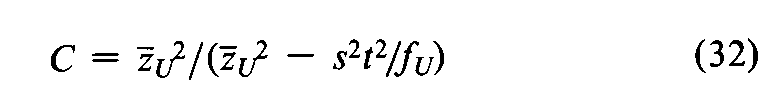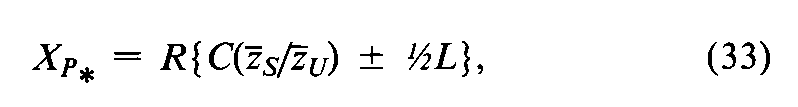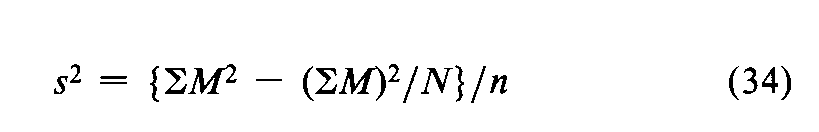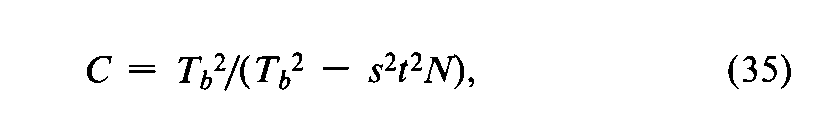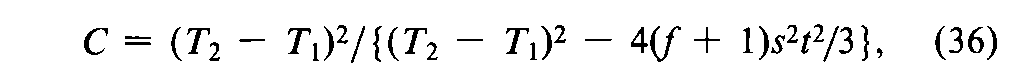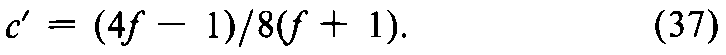The Confidence Interval and Limits of Potency
Abioassay provides an estimate of the true potency of an Unknown.This estimate falls within a confidence interval,which is computed so that the odds are not more than 1in 20(P=0.05)that the true potency either exceeds the upper limit of the confidence interval or is less than its lower limit.Since this interval is determined by a number of factors that may influence the estimate of potency,the required precision for most bioassays is given in the monograph in terms of the confidence interval,related either to the potency directly or to its logarithm.
General Calculation—
Despite their many forms,bioassays fall into two general categories:(1)those where the log-potency is computed directly from a mean or a mean difference,and (2)those where it is computed from the ratio of two statistics.
(1)When the log-potency of an assay is computed as the mean of several estimated log-potencies that are approximately equal in precision,the log-confidence interval is
where sis the standard deviation of a single estimated log-potency,tis read from Table 9with the ndegrees of freedom in s,and kis the number of estimates that have been averaged.The same equation holds where the log-potency is computed as the mean bar(x)of kdifferences x,with sthe standard deviation of a single x.In either case,the estimated log-potency Mis in the center of its confidence interval,so that its confidence limits are
The upper and lower limits are converted to their antilogarithms to obtain the limits as explicit potencies.
(2)More often,the log-potency or potency is computed from a ratio,and in these cases the length of the confidence interval is typified by the log-interval in the equation
whereM¢is the log-relative potency as defined (see Calculation of Potency from a Single Assay),iis the log-interval between successive doses,and c¢is a constant characteristic of the assay procedure.The remaining term Cdepends upon the precision with which the slope of the dosage-response curve has been determined.(This is sometimes expressed in terms of g =(C–1)/C.)In factorial assays,it is computed as
where s2is the error variance of a single observation,t2is read from Table 9with the degrees of freedom in s2,fis the number of responses in each Ttused in calculating Tb,and Tband ebare computed with the factorial coefficients for row bin Tables 6to 8.The s2in Equation 26depends upon the design of the assay,as indicated for each drug in the next section.In a valid assay,Cis a positive number.
In an assay of two or more Unknowns against a common Standard,all with dosage-response curves that are parallel within the experimental error,Cmay be computed with the error variance s2for the assay and with the assay slope as
The slope factor Tb¢=S(x1Tt)or S(x1y)for each of the h¢preparations,including the Standard,is computed with the factorial coefficients x1for the Standard in the appropriate row bof Table 6or 8.If a treatment total Ttincludes one or more replacements for a missing response,replace ebfin Equation 27,or ebfh¢/2in Equation 28,by f2S(x12/f¢),where each x1is a factorial coefficient in row bof Tables 6to 8,in this chapter,and f¢is the number of responses in the corresponding Ttbeforeadding the replacement.With this C,compute the confidence interval as
In assays computed from a ratio,the most probable log-potency Mis not in the exact center of the confidence interval.The upper and lower confidence limits in logarithms are
Cis often very little larger than unity,and the more precise the assay,the more nearly Capproaches 1exactly.R=zS/zUis the ratio of corresponding doses of the Standard and of the Unknown or the assumed potency of the Unknown.The upper and lower confidence limits in log-potencies are converted separately to their antilogarithms to obtain the corresponding potencies.
Confidence Intervals for Individual Assays—
Since the confidence interval may vary in detail from the above general patterns,compute it for each assay by the special directions given under the name of the substance in the paragraphs following.
Antibiotic Assays—
The confidence interval may be computed by Equations 24and 25.
Calcium Pantothenate—
For log-potencies obtained by interpolation from the Standard curve,the confidence interval may be computed with Equations 19and 24.For log-potencies calculated with Equation 8or 10,s2may be computed with Equation 15,Cwith Equation 27or 28,and the confidence interval Lwith Equation 26or 29.
Corticotropin Injection—
Compute the log confidence interval by Equations 26and 27,with the coefficients and constants in Table 6for a 3-dose assay,and s2as determined by Equation 13or 14.
Digitalis—
Compute the confidence interval as
where fUand fSare the number of observations on the Unknown and on the Standard,and
is determined with s2from Equation 11.The confidence limits for the potency in USP Units are then
in which Ris as defined in the Glossary of Symbols.
Glucagon for Injection—
Compute the error variance s2by Equation 15a,Cby Equation 27with ebf =16n¢,and the log confidence interval Lby Equation 26with c¢i2=0.09062.
Chorionic Gonadotropin—
Proceed as directed under Corticotropin Injection.
Heparin Sodium—
If two independent determinations of the log-potencyMdiffer by more than 0.05,carry out additional assays and compute the error variance among the Nvalues of Mas
with n =N–1degrees of freedom.Given this value,determine the confidence interval in logarithms (L)by Equation 24.
Insulin Injection—
Compute the error variance (s2)of yby Equation 16and Cas
where t2from Table 9depends upon n=4(f–1)degrees of freedom in s2and N=4fis the total number of differences in the four groups.By Equation 26,compute the confidence interval Lin logarithms,where c¢i2=0.09062.The upper and lower confidence limits in USP Units of insulin are given by the antilogarithms of XMfrom Equation 30.
Oxytocin Injection—
Compute the approximate log confidence interval by Equation 26,in which
where s2is defined by Equation 18,and
Tubocurarine Chloride Injection—
Compute the error variance by Equation 12,and the confidence interval by Equation 24.
Vasopressin Injection—
Compute the error variance s2by Equation 16,Cby Equation 35,and the log confidence interval by Equation 26,where c¢=1and iis the log-interval separating the two dosage levels.
Vitamin B12Activity—
Proceed as directed under Calcium Pantothenate.