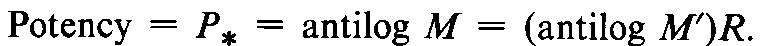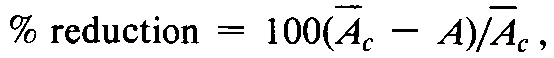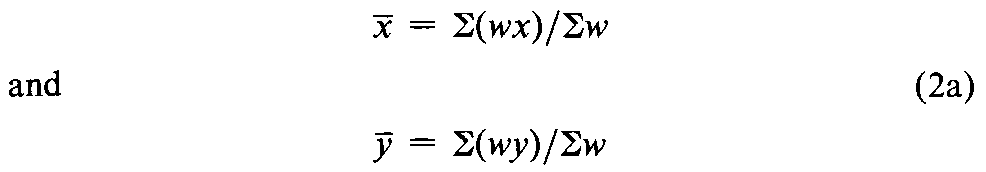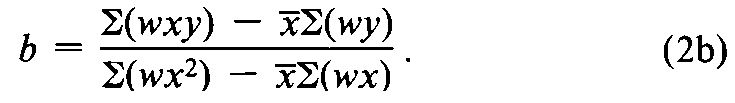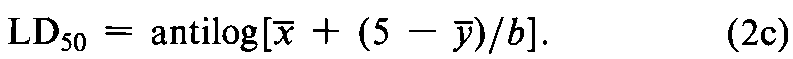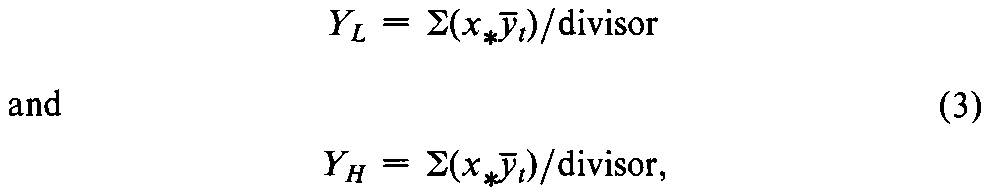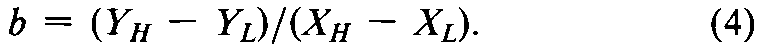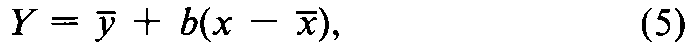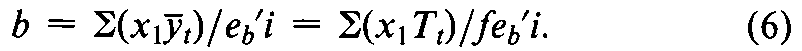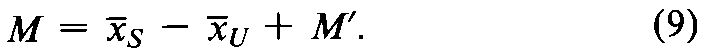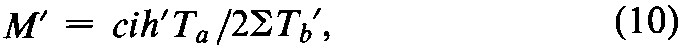Calculation of Potency from a Single Assay
Directions for calculating potency from the data of a single assay are given in the individual monographs.In those assays that specify graphical interpolation from dosage-response curves but that meet the conditions for assay validity set forth herein,potency may be computed alternatively by the appropriate method in this section.
Planning the assay involves assigning to the Unknown an assumed potency,to permit administering it in dosages equivalent to those of the Standard.The closer the agreement between this original assumption and the result of the assay,the more precise is the calculated potency.The ratio of a given dose of the Standard,in µg or in USP Units,to the corresponding dose of the Unknown,measured as specified in the monograph,is designated uniformly by R.The log-relative potency in quantities assumed initially to equal those of the Standard is designated asM¢.
Ideally,M¢should not differ significantly from zero.The log-potency is
or
Assay from Direct Determinations of the Threshold Dose—
Tubocurarine Chloride Injection and Metocurarine Iodide are assayed from the threshold dose that just produces a characteristic biological response.The ratio of the mean threshold dose for the Standard to that for the Unknown gives the potency directly.The threshold dose is determined twice in each animal,once with the Standard and once with the Unknown.Each dose is converted to its logarithm,the difference (x)between the two log-doses is determined for each animal,and potency is calculated from the average of these differences.
In the Bacterial Endotoxins Test á85ñ,the geometric mean dilution endpoint for the Unknown corresponding to the geometric mean dilution endpoint for the Standard (multiplied by a dilution factor,where applicable)gives the concentration of endotoxin in the test material.
In these assays,the confidence interval depends upon the variability in the threshold dose.
Indirect Assays from the Relationship between the Log-Dose and the Response—
Generally,the threshold dose cannot be measured directly;therefore,potency is determined indirectly by comparing the responses following known doses of the Standard with the responses following one or more similar doses of the Unknown.Within a restricted dosage range,a suitable measure of the response usually can be plotted as a straight line against the log-dose,a condition that simplifies the calculation of potency and its confidence interval.Both the slope and position of the log-dose response relationship are determined in each assay by the use of two or more levels of the Standard,or,preferably,of both the Standard and the Unknown.
In the assay of Heparin Sodium,the interval between the dose at which clotting occurs and that which produces no clotting is so small that the dosage-response curve is not determined explicitly.Moving averages are used instead to interpolate the log-dose corresponding to 50%clotting for both the Standard and the Unknown,leading to the log-potency (see Calculationunder Heparin Sodium).The precision of the potency is estimated from the agreement between independent assays of the same Unknown.
For a drug that is assayed biologically,the response should plot as a straight line against the log-dose over an adequate range of doses.Where a preliminary test is required or the assay depends upon interpolation from a multi-dose Standard curve,plot on coordinate paper the mean response of the Standard at each dosage level on the ordinate against the log-dose xon the abscissa.If the trend is basically linear over the required dosage range,the initial response unit may be used directly as y;if,instead,the trend is clearly curvilinear,a suitable transformation of each initial reading may bring linearity.
One possible transformation is to logarithms;another,in microbial tube assays,where y=(100–%transmittance)does not plot linearly against the log-dose x,is to probits.In this case,if absorbance cannot be read directly,the percent transmittance for each tube or test solution is first converted to absorbance,A=2-log(%transmittance).Each absorbance value,in turn,is converted to %reduction in bacterial growth as
where bar(A)cis the mean density for the control tubes (without antibiotic or with excess of vitamin)in the same set or tube rack.Percent reduction is then transformed to a probit (see Table 3)to obtain a new yfor all later calculation.The probit transformation offers the advantage of extending the working range of linearity even where a portion of the dosage-response relationship is nonlinear in the original units of percent transmittance,provided that the incubation period does not extend beyond the logarithmic phase of growth of the control tubes.
Table 3
| Probits (normal deviates +5)corresponding to percentages in the margins. | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | — | 2.67 | 2.95 | 3.12 | 3.25 | 3.36 | 3.45 | 3.52 | 3.59 | 3.66 |
| 10 | 3.72 | 3.77 | 3.82 | 3.87 | 3.92 | 3.96 | 4.01 | 4.05 | 4.08 | 4.12 |
| 20 | 4.16 | 4.19 | 4.23 | 4.26 | 4.29 | 4.33 | 4.36 | 4.39 | 4.42 | 4.45 |
| 30 | 4.48 | 4.50 | 4.53 | 4.56 | 4.59 | 4.61 | 4.64 | 4.67 | 4.69 | 4.72 |
| 40 | 4.75 | 4.77 | 4.80 | 4.82 | 4.85 | 4.87 | 4.90 | 4.92 | 4.95 | 4.97 |
| 50 | 5.00 | 5.03 | 5.05 | 5.08 | 5.10 | 5.13 | 5.15 | 5.18 | 5.20 | 5.23 |
| 60 | 5.25 | 5.28 | 5.31 | 5.33 | 5.36 | 5.39 | 5.41 | 5.44 | 5.47 | 5.50 |
| 70 | 5.52 | 5.55 | 5.58 | 5.61 | 5.64 | 5.67 | 5.71 | 5.74 | 5.77 | 5.81 |
| 80 | 5.84 | 5.88 | 5.92 | 5.95 | 5.99 | 6.04 | 6.08 | 6.13 | 6.18 | 6.23 |
| 90 | 6.28 | 6.34 | 6.41 | 6.48 | 6.55 | 6.64 | 6.75 | 6.88 | 7.05 | 7.33 |
| 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
| 99 | 7.33 | 7.37 | 7.41 | 7.46 | 7.51 | 7.58 | 7.65 | 7.75 | 7.88 | 8.09 |
The LD50in the Safetytest for Iron Dextran Injectionis calculated with log-doses and probits.The four doses of the Injection,in mg of iron per kg of body weight,are transformed to x1=2.574,x2=2.699,x3=2.875,and x4=3.000.The probits corresponding to the number of deaths observed in each group of 10mice are designated y1,y2,y3,and y4,respectively,and are given in Table 3for mortalities from 10to 90percent.For observed deaths of 0and 10adjacent to doses giving an intermediate mortality,use the approximate probits 3.02and 6.98,respectively;omit the end value (at x1or x4)if not adjacent to an intermediate mortality.Since the information in a probit varies with its expectation,assign each probit an approximate relative weight wfor computing the LD50of the Injection,as shown in the accompanying table.
| No.of Deaths | 0or 10 | 1or 9 | 2or 8 | 3or 7 | 4to 6 |
| Weight,w | 0.3 | 0.7 | 1.0 | 1.2 | 1.3 |
Calculate the weighted means
from the sum of the weights,Sw,of the four (or three)acceptable responses and the corresponding weighted sums of the log-doses,S(wx),and of the probits,S(wy).From the sums of the weighted products,S(wxy),and of the weighted squares,S(wx2),compute the slope bof the log-dose-probit line as
The LD50for this safety test,in mg of iron per kg of body weight,is calculated as
In quantal assays not included in this Pharmacopeia,such as the mouse assay for insulin,the calculation with probits involves other adjustments that are omitted here.
When the mean response bar(y)tfor each dose of Standard plots linearly against the log-dose,and the kdoses are spaced at equal intervals on the logarithmic scale,the predicted responses (YLand YH)at the extreme ends of the line of best fit can be computed directly with the coefficients x*in Table 4,which correspond to the ksuccessive log-doses,as
where Sstands uniformly for “the sum of”the values that follow it.When YLand YHare plotted against the low and high log-doses,XLand XH,respectively,they may be connected by a straight line with the slope
At any selected log-dose xof Standard,the predicted response is
where bar(x)=Sx/k,and bar(y)=(YL+YH)/2,or,for predictions within a set,bar(y)is the mean response for the Standard within the set.
Table 4
| Coefficients x*for computing the responses YLand YHpredicted by least squares at the lowest and highest of klog-doses when these are spaced at equal intervals. | ||||||||
| No.of Doses | Predicted End Y | Coefficient x*for Mean Response bar(y)tat Log-Dose | Divisor | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| 3 | YL | 5 | 2 | -1 | 6 | |||
| YH | -1 | 2 | 5 | 6 | ||||
| 4 | YL | 7 | 4 | 1 | -2 | 10 | ||
| YH | -2 | 1 | 4 | 7 | 10 | |||
| 5 | YL | 3 | 2 | 1 | 0 | -1 | 5 | |
| YH | -1 | 0 | 1 | 2 | 3 | 5 | ||
| 6 | YL | 11 | 8 | 5 | 2 | -1 | -4 | 21 |
| YH | -4 | -1 | 2 | 5 | 8 | 11 | 21 | |
When the log-dose response relationship is linear,but the kdoses (expressed in mL)are spaced substantially in an arithmetic sequence as in Table 5(which refers to the microbial assays set forth under Antibiotics—Microbial Assays á81ñ),the slope bof the straight line of best fit may be computed with the terms in Table 5and the mean response at each dose bar(y)t,or Tt=fbar(y)twhere the number of y's(f)is constant at each dose,as
The coefficients x1are convenient multiples of the differences (x -bar(x))about the mean log-dose bar(x),and eb¢iis the corresponding multiple of S(x -bar(x))2.The predicted response Yat a given log-dose xmay be computed by substitution of the assay slope bin Equation 5and of the mean bar(y)either of all the responses on the Standard in the entire assay or of those for each set separately.
Table 5
| Coefficients x1for computing the slope bof a log-dose response curve when the doses are spaced on an arithmetic scale as shown. | ||||||||
| Coefficients x1for Computing bfrom the Responses yat Doses,in mL,of | ||||||||
| No.of Doses | 1 | 1.5 | 2 | 3 | 4 | 5 | Divisor eb¢i | Mean Log-Dose bar(x) |
| 4 | — | –29 | –12 | 12 | 29 | — | 14.4663 | 0.38908 |
| 5 | –34 | — | –9 | 5 | 15 | 23 | 24.7827 | 0.41584 |
| 5 | — | –20 | –11 | 2 | 11 | 18 | 13.3249 | 0.45105 |
| 6 | –15 | –8 | –3 | 4 | 9 | 13 | 14.1017 | 0.37588 |
POTENCIES INTERPOLATED FROM A STANDARD CURVE—
Where the log-dose response curve of the Standard in a given assay is curvilinear and is fitted graphically to the plotted points,the amount of Standard that would be expected to produce each observed response yof an Unknownis estimated by interpolation from the curve and then adjusted for the known concentration of its test solution.
When the response to the Standard can be plotted linearly against the log-dose,it is fitted numerically by a straight line,as described in the preceding section.For assays in randomized sets,a standard curve is computed with bfor the assay and bar(y)for each set and the response yUin each tube of a given Unknownin that set is converted to an estimated log-relative potency,
where YSis the response predicted by the standard curve at the assumed log-dose xof the Unknown.The average of the separate estimates from each of fsets,M¢=SX/f,is the assayed log-relative potency of the Unknown.
Factorial Assays from the Response to Each Treatment—
When some function of the response can be plotted linearly against the log-dose,the assayed potency is computed from the total response for each treatment,and its precision is measured in terms of confidence intervals.This requires that (1)in suitable units the response (y)depends linearly upon the log-dose within the dosage range of the assay,and (2)the number (f)of responses be the same at each dosage level of both Standard and Unknown.The y's are totaled at each dosage level of each preparation.In different combinations,these totals,Tt,lead directly to the log-relative potency and to tests of assay validity.The factorial coefficients in Tables 6,7,and 8determine how they are combined.In a given row,each Ttis multiplied by the corresponding coefficient and the products summed to obtain Ti.The Ti's in the successive rows carry the same meaning in all assays.
Table 6
| Factorial coefficients x1for analyzing a balanced bioassay,in which successive log-doses of Standard (Si)and of Unknown (Ui)are spaced equally,each with the same number (f)of responses totaling Tt. | |||||||||||
| Factorial Coefficients x1for Each Dose | |||||||||||
| Design | Row | S1 | S2 | S3 | S4 | U1 | U2 | U3 | U4 | ei | Ti |
| 2,2 | a | -1 | -1 | 1 | 1 | 4 | Ta | ||||
| b | -1 | 1 | -1 | 1 | 4 | Tb | |||||
| ab | 1 | -1 | -1 | 1 | 4 | Tab | |||||
| 3,3 | a | -1 | -1 | -1 | 1 | 1 | 1 | 6 | Ta | ||
| b | -1 | 0 | 1 | -1 | 0 | 1 | 4 | Tb | |||
| ab | 1 | 0 | -1 | -1 | 0 | 1 | 4 | Tab | |||
| q | 1 | -2 | 1 | 1 | -2 | 1 | 12 | Tq | |||
| aq | -1 | 2 | -1 | 1 | -2 | 1 | 12 | Taq | |||
| 4,4 | a | -1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 | 8 | Ta |
| b | -3 | -1 | 1 | 3 | -3 | -1 | 1 | 3 | 40 | Tb | |
| ab | 3 | 1 | -1 | -3 | -3 | -1 | 1 | 3 | 40 | Tab | |
| q | 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 | 8 | Tq | |
| aq | -1 | 1 | 1 | -1 | 1 | -1 | -1 | 1 | 8 | Taq | |
| Value of Constant for Design | |||||
| For Computing | Equation No. | Constant | 2,2 | 3,3 | 4,4 |
| M¢ | 8,10 | c | 1 | 4/3 | 5 |
| L | 26,29 | c¢ | 1 | 8/3 | 5 |
Tain the first row measures the difference in the average response to the Standard and to the Unknown.Tbin the second row leads directly to the combined slope of the dosage-response curves for both Standard and Unknown.The third to the fifth rows (ab,q,and aq)provide tests for the validity of an assay,as described in a later section.From the totals Taand Tb,compute the log-relative potency of the Unknown,before adjustment for its assumed potency,as
where iis the interval in logarithms between successive log-doses of both the Standard and the Unknown,and the constant cis given separately at the bottom of each table.EachM¢is corrected to its log-potencyMby Equation 2.
When doses are spaced unequally on a log scale,as in Table 8,use instead the constant ciat the bottom of the table.
Table 7
| Factorial coefficients x1for analyzing a partially balanced assay,in which successive log-doses of Standard (Si)and of Unknown (Ui)are spaced equally,each with the same number (f)of responses totaling Tt.If the number of successive doses of the Unknown exceeds by one the number on the Standard,interchange Siand Uiin the heading and reverse all signs in rows a,ab,and aq. | ||||||||||
| Factorial Coefficients x1for Each Dose | ||||||||||
| Design | Row | S1 | S2 | S3 | S4 | U1 | U2 | U3 | ei | Ti |
| 2,1 | a | -1 | -1 | 2 | 6 | Ta | ||||
| b | -1 | 1 | 0 | 2 | Tb | |||||
| 3,2 | a | -2 | -2 | -2 | 3 | 3 | 30 | Ta | ||
| b | -2 | 0 | 2 | -1 | 1 | 10 | Tb | |||
| ab | 1 | 0 | -1 | -2 | 2 | 10 | Tab | |||
| q | 1 | -2 | 1 | 0 | 0 | 6 | Tq | |||
| 4,3 | a | -3 | -3 | -3 | -3 | 4 | 4 | 4 | 84 | Ta |
| b | -3 | -1 | 1 | 3 | -2 | 0 | 2 | 28 | Tb | |
| ab | 3 | 1 | -1 | -3 | -5 | 0 | 5 | 70 | Tab | |
| q | 3 | -3 | -3 | 3 | 2 | -4 | 2 | 60 | Tq | |
| aq | -1 | 1 | 1 | -1 | 1 | -2 | 1 | 10 | Taq | |
| Value of Constant for Design | |||||
| For Computing | Equation No. | Constant | 2,1 | 3,2 | 4,3 |
| M¢ | 8,10 | c | 1/2 | 5/6 | 7/6 |
| L | 26,29 | c¢ | 3/4 | 25/12 | 49/12 |
Table 8
| Factorial coefficients x1for analyzing assays with a 3-or 4-dose sequence of 1.5,2.0,3.0,and 4.0,each dose having the same number (f)of responses. | |||||||||||
| Dose of Standard | Dose of Unknown | ||||||||||
| Design | Row | 1.5 | 2.0 | 3.0 | 4.0 | 1.5 | 2.0 | 3.0 | 4.0 | ei | Ti |
| 4,4 | a | -1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 | 8 | Ta |
| b | -29 | -12 | 12 | 29 | -29 | -12 | 12 | 29 | 3940 | Tb | |
| ab | 29 | 12 | -12 | -29 | -29 | -12 | 12 | 29 | 3940 | Tab | |
| q | 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 | 8 | Tq | |
| aq | -1 | 1 | 1 | -1 | 1 | -1 | -1 | 1 | 8 | Taq | |
| 3,3 | a | -1 | -1 | -1 | 1 | 1 | 1 | 6 | Ta | ||
| b | -25 | -3 | 28 | -25 | -3 | 28 | 2836 | Tb | |||
| ab | 25 | 3 | -28 | -25 | -3 | 28 | 2836 | Tab | |||
| q | 31 | -53 | 22 | 31 | -53 | 22 | 8508 | Tq | |||
| aq | -31 | 53 | -22 | 31 | -53 | 22 | 8508 | Taq | |||
| 3,3 | a | -1 | -1 | -1 | 1 | 1 | 1 | 6 | Ta | ||
| b | -28 | 3 | 25 | -28 | 3 | 25 | 2836 | Tb | |||
| ab | 28 | -3 | -25 | -28 | 3 | 25 | 2836 | Tab | |||
| q | 22 | -53 | 31 | 22 | -53 | 31 | 8508 | Tq | |||
| aq | -22 | 53 | -31 | 22 | -53 | 31 | 8508 | Taq | |||
| Value of Constant for Design | ||||
| For Computing | Equation No. | Constant | 4,4 | 3,3 |
| M¢ | 8,10 | ci | 7.2332 | 5.3695 |
| L | 26,29 | c¢i2 | 0.10623 | 0.06100 |
In a fully balanced assay,such as the assay for corticotropin,compute M¢with the coefficients in Table 6.If one preparation has one less dose than the other but the successive log-doses of both Standard and Unknown differ by a constant interval i,use the factorial coefficients in Table 7,correcting for the actual difference between the observed mean log-doses,bar(x)Sand bar(x)U,by computing
In assays where the successive doses are not spaced at equal log-intervals,the log-relative potency of a single Unknown may be computed by Equation 8with the factorial coefficients and ciin Table 8.
In an assay of two or more Unknowns against a common Standard,all with dosage-response lines that are parallel within the experimental error,each log-relative potency may be computed with the same assay slope as follows.For each preparation,determine the slope factor Tb¢=S(x1Tt)or S(x1y),where the values of x1are the factorial coefficients for the Standard in the appropriate row bof Table 6or 8.The log-relative potency of each Unknown is
where h¢is the number of values of Tb¢summed in the denominator.
Assays from Differences in Response—
When doses of the Standard and Unknown are paired and the difference in response is computed for each pair,these differences are not affected by variations in the average sensitivity of the paired readings.The paired 2-dose insulin assay corresponds to the first design in Table 6,and requires four equal groups of rabbits each injected twice (see Insulin Assays á121ñ).The difference (y)in the blood sugar response of each rabbit to the two treatments leads to the log-relative potencyM¢(see the first two paragraphs of the section,Calculation of Potency from a Single Assay).The Vasopressin Injection assay follows a similar design,substituting two or more randomized sets of four successive pairs of injections into rats for the four treatment groups of rabbits in the insulin assay.
Oxytocin Injection is assayed from blood pressure changes in a single test animal following alternating injections of a single dose of Standard and of one of two doses of the Unknown.The calculation of potency from the differences in the response of the Unknown and to the average of the two adjacent responses to the Standard is equivalent to the first design in Table 7with Sand Ureversed,where iis the log-interval between the two dosage levels of the Unknown.